本記事は、統計学のテキストの内容をRでコード実装するシリーズです。
この記事で扱うデータおよび度数分布表の考え方は、小島寛之著『完全独習 統計学入門』(ダイヤモンド社)を参考にしています。
今回は、上記テキストで示されている度数分布表とヒストグラムの作成手順を、Rで実装することを目的に整理しました。
実行環境
実行環境は以下の通りです。
| 項目 | バージョン |
|---|---|
| OS | Windows 11 Home 64bit (バージョン 24H2) |
| R | 4.5.1 |
| RStudio | 2025.09.0 |
参考文献
参考図書はこちらです。
また、以下の記事も参考にさせていただきました。
データの準備
本書 P.16に掲載されている身長データ(図表1-1)を使用します。
# 身長データ(単位:cm)
height_cm <- c(
151, 154, 158, 162,
154, 152, 151, 167,
160, 161, 155, 159,
160, 160, 155, 153,
163, 160, 165, 146,
156, 153, 165, 156,
158, 155, 154, 160,
156, 163, 148, 151,
154, 160, 169, 151,
160, 159, 158, 157,
154, 164, 146, 151,
162, 158, 166, 156,
156, 150, 161, 166,
162, 155, 143, 159,
157, 157, 156, 157,
162, 161, 156, 156,
162, 168, 149, 159,
169, 162, 162, 156,
150, 153, 159, 156,
162, 154, 164, 161
)データ数nを確認します。
# データ数の確認
n <- length(height_cm)
n## [1] 80length() 関数は、ベクトルに含まれる要素の個数を返します。ここでは 80 人分の身長データを扱っていることが分かります。
度数分布表の作成
度数分布表を作成する流れは以下の通りです。
- データの範囲(最小値・最大値)の確認
- 階級幅と境界の設定
- 階級ラベルの作成
- 階級値の決定
- 階級の割り当て
- 度数の集計
- 度数分布表として整形
- 相対度数・累積度数の追加
1. データの範囲(最小値・最大値)の確認
まずは、データの範囲を把握します。
# 最小値・最大値の確認
min_height_cm <- min(height_cm)
max_height_cm <- max(height_cm)
min_height_cm
max_height_cm## [1] 143
## [1] 169min() は最小値、max() は最大値を返す関数です。今回のデータでは、最小値 143 cm、最大値 169 cmでした。
2. 階級幅と境界の設定
階級(class)の対象範囲は、最小値から最大値まで包含するように、140から170と設定することにします。
階級幅(class interval)は、分析の目的によって決め方が変わります。今回は学習用として、身長データとして直感的に理解しやすい 5 cm 刻みを採用します。
# 階級の対象範囲
start_val <- 140 #開始値(最小値より少し小さいキリの良い数)
end_val <- 170 #終了値(最大値より少し大きいキリの良い数)
# 階級幅の設定
class_interval <- 5次に、階級の境界となる数値(breaks)を設定します。
# 整数データを整数区間に割り当てやすくするためのずらし
offset <- 0.5
# 階級境界を作成
class_breaks <- seq(
from = start_val + offset,
to = end_val + offset,
by = class_interval
)
class_breaks## [1] 140.5 145.5 150.5 155.5 160.5 165.5 170.5なぜ0.5ずらすのか?
度数分布表を「141–145」「146–150」のような 整数の区間で作りたい場合、境界を「150」ジャストに設定してしまうと、「150という値は下の階級に入るのか?上の階級に入るのか?」という曖昧さが生じます。
境界を 150.5 のように設定すれば、以下のように迷うことなく自動的に振り分けることができます(連続性の補正)。
- 150 は 150.5 より小さい → 下の階級
- 151 は 150.5 より大きい → 上の階級
今回は整数データなので、ずらさなくても正しい階級に割り当てられますが、整数区間ラベルを作るために0.5ずらしています
seq() 関数とは
seq() 関数は 、一定の間隔で並んだ数値の列を作る関数です。
from:開始値to:終了値by:増分
今回のコードは、「140.5 から 170.5 までを 5 ずつ増やしながら並べる」という指示になります。
3. 階級ラベルの作成
class_breaks をもとに階級ラベルを作成します。
コードを書く前に、まずは「最終的にどのような階級を作りたいのか」を整理しておくと、実装が分かりやすくなります。今回作成する階級ラベルは、以下の通りです。
- 141–145
- 146–150
- 151–155
- 156–160
- 161–165
- 166–170
# 下端の計算
lower_bounds <- floor(class_breaks[-length(class_breaks)]) + 1
# 上端の計算
upper_bounds <- floor(class_breaks[-1])
# 文字列として結合
class_labels <- paste(
lower_bounds,
upper_bounds,
sep = "-"
)
class_labels## [1] "141-145" "146-150" "151-155" "156-160" "161-165" "166-170"floor()関数は、小数点以下を切り捨てる関数です。
class_breaks[-1] は、「1 番目の要素を除いた残りすべて」を意味します。同様に、class_breaks[-length(class_breaks)] は、「最後の要素を除いた残りすべて」を意味します。
R ではインデックス指定において、
- 正の数:その位置の要素を取り出す
- 負の数:その位置の要素を除外する
というルールがあるため、このように書くことができます。
paste() 関数 は、複数の値を文字列として結合する関数です。sep = "-" を指定することで、下端値と上端値の間をハイフンで結んだ階級ラベルを作成しています。
4. 階級値の決定
階級値(class mark)は、各階級の代表値として用いる「区間の中央の値」のことです。一般的に、以下のように求められます。
# 階級値の決定
class_marks <- (lower_bounds + upper_bounds) / 2
class_marks## [1] 143 148 153 158 163 1685. 階級の割り当て
次に、各データがどの階級に属するかを割り当てます。
# 身長データを階級ごとに分類
height_class <- cut(
height_cm, # 対象データ
breaks = class_breaks, # さっき作った境界(140.5, 145.5...)
labels = class_labels, # 階級ラベル(141-145...)
include.lowest = TRUE # 最初の区間だけ下端も含める
right = TRUE, # (a, b] つまり右側を含む設定(今回は.5なので厳密には不要だが明示)
)
# 先頭データを確認
head(height_class)## [1] 151-155 151-155 156-160 161-165 151-155 151-155
## Levels: 141-145 146-150 151-155 156-160 161-165 166-170cut() 関数は、連続した数値データを指定した区間に分割し、各値がどの区間に属するかを示す因子(factor)として返します。cut()関数 の戻り値は数値ではなく「区間ラベル(カテゴリ)」であることが重要です。
right = TRUE は区間を (a, b](右端を含む)として扱う指定です。今回は境界が 145.5 のような小数で、データは整数のため境界値に一致しにくく、結果が変わらないことが多いですが、階級の定義として重要なので明示しています。include.lowest = TRUEは最初の区間だけ下端も含める指定で、最小値が境界に一致したときの取りこぼしを防ぎます。
6. 度数の集計
階級ごとの度数(Frequency)を数えます。
# 各階級の度数を数える
class_freq <- table(height_class)
class_freq
sum(class_freq) # 度数の合計## 141-145 146-150 151-155 156-160 161-165 166-170
## 1 6 19 30 18 6
## [1] 80table() 関数は、同じ値の出現回数を集計する関数です。
度数の合計が、データ数(length(height_cm))と一致していれば、全データが必ずどこかの階級に割り当てられていることが確認できます。
7. 度数分布表として整形
table() の戻り値は名前付きベクトルです。これは簡単な確認には便利ですが、後続の処理(他の列との結合、可視化、集計など)を考えると、データフレーム形式の方が扱いやすいため、ここで変換しておきます。
# データフレームに変換
freq_df <- data.frame(
class = class_labels, # 階級
class_marks = class_marks, # 階級値
freq = as.integer(class_freq) # 度数
)
freq_df## class class_marks freq
## 1 141-145 143 1
## 2 146-150 148 6
## 3 151-155 153 19
## 4 156-160 158 30
## 5 161-165 163 18
## 6 166-170 168 6table() 関数が返す値は、見た目は数値に見えますが、内部的には特殊な属性を持つオブジェクトです。そのため、as.integer(class_freq)によって明示的に整数型に変換しています。
8. 相対度数・累積度数の計算
- 相対度数 (relative freqquency):各階級の度数が、全体に占める割合(度数 / 全体データ数)
- 累積度数 (cumulative frequency):その階級以下に含まれる度数を、上から順に合計したもの
# 相対度数と累積度数の計算
relative_freq <- freq_df$freq / sum(freq_df$freq)
cumulative_freq <- cumsum(freq_df$freq)
relative_freq
cumulative_freq
sum(relative_freq) #相対度数の合計## [1] 0.0125 0.0750 0.2375 0.3750 0.2250 0.0750
## [1] 1 7 26 56 74 80
## [1] 1cumsum() は 累積和(cumulative sum) を計算する関数です。第1階級から順に足し上げることで累積度数になります。
相対度数の合計は、理論上 1 になります。多少のズレが出る場合は、丸め誤差によるものです。
最後に、計算結果を度数分布表に追加します。
# 度数分布表に追加
freq_df$relative_freq <- relative_freq
freq_df$cumulative_freq <- cumulative_freq
freq_df## class class_marks freq relative_freq cumulative_freq
## 1 141-145 143 1 0.0125 1
## 2 146-150 148 6 0.0750 7
## 3 151-155 153 19 0.2375 26
## 4 156-160 158 30 0.3750 56
## 5 161-165 163 18 0.2250 74
## 6 166-170 168 6 0.0750 80これで、度数分布表が完成しました。
ヒストグラムの作成
度数分布表で使用したclass_breaksをそのままhist()関数に渡すことで、表と整合性の取れたグラフを描画します。
# ヒストグラムの作成
hist(
height_cm,
breaks = class_breaks, # 作成した境界を使用
include.lowest = TRUE,
right = TRUE, # cut()の挙動に合わせる((a, b]区間)
xaxt = "n" # デフォルトのx軸を消す
)
axis(
side = 1,
at = class_marks, # 目盛の位置(棒の中心)
labels = class_marks # 表示ラベル
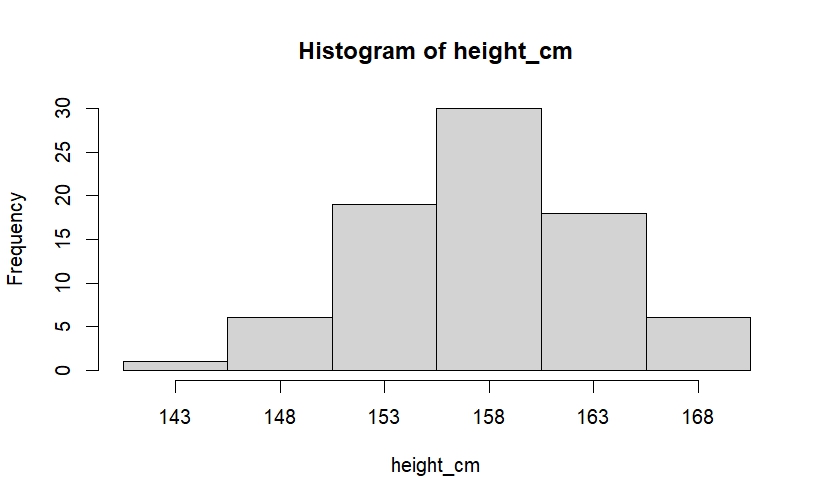
)hist() 関数は、内部で階級境界(breaks)を解釈し、各階級の度数を数え上げたうえで描画します。
hist() の戻り値($counts, $mids, $breaks)を確認すると、度数分布表で計算した度数や階級値と対応していることが分かります。
練習問題
本書 P.23に掲載されている体重データ(図表1-4)から、上記と同じ方法で度数分布表とヒストグラムを作成してみます。
# 体重データ(単位:kg)
weight_kg <- c(
48, 54, 47, 50, 53, 43, 45, 43,
44, 47, 58, 46, 46, 63, 49, 50,
48, 43, 46, 45, 50, 53, 51, 58,
52, 53, 47, 49, 45, 42, 51, 49,
58, 54, 45, 53, 50, 69, 44, 50,
58, 64, 40, 57, 51, 69, 58, 47,
62, 47, 40, 60, 48, 47, 53, 47,
52, 61, 55, 55, 48, 48, 46, 52,
45, 38, 62, 47, 55, 50, 46, 47,
55, 48, 50, 50, 54, 55, 48, 50
)
length(weight_kg)## [1] 80結果は、以下のようになりました。
## 体重データの度数分布表
## class class_marks freq relative_freq cumulative_freq
## 1 36-40 38 3 0.0375 3
## 2 41-45 43 11 0.1375 14
## 3 46-50 48 33 0.4125 47
## 4 51-55 53 19 0.2375 66
## 5 56-60 58 7 0.0875 73
## 6 61-65 63 5 0.0625 78
## 7 66-70 68 2 0.0250 80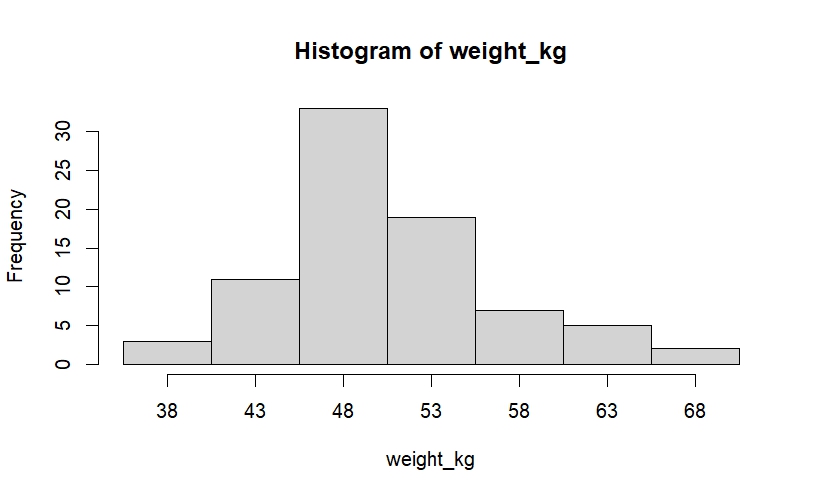
まとめ
今回ご紹介したRで度数分布表を作成する手順をまとめると、以下のようになります。
- データの確認:
min()とmax()で最小・最大値を確認し、階級の対象範囲を決める - 階級境界の設定:
seq()関数で区切り(境界値)を作る - ラベルと階級値の作成:
paste()で「141-145」といった表示用ラベルを作り、各区間の中央値を階級値として算出する - データの分類:
cut()関数を使い、各データを設定した階級に振り分ける - 度数の集計:
table()関数で各階級のデータ数を数え上げる - 表の整形と列の追加:
data.frame()で表形式にまとめ、相対度数や累積度数を追加する
1から度数分布表を作成するのと比べて、ヒストグラムは比較的簡単に作成できるのが意外でした。
ただ、度数分布表の作成の過程でhist()関数の処理の流れが分かり、理解が深まりました。



