本記事は、統計学のテキストの内容をRでコード実装するシリーズです。
この記事で扱うデータおよび度数分布表の考え方は、小島寛之著『完全独習 統計学入門』(ダイヤモンド社)を参考にしています。
今回は、上記テキストで示されている「度数分布表から平均値を求める考え方」について、R を用いて具体的に確認することを目的とします。
実行環境
実行環境は以下の通りです。
| 項目 | バージョン |
|---|---|
| OS | Windows 11 Home 64bit (バージョン 24H2) |
| R | 4.5.1 |
| RStudio | 2025.09.0 |
参考文献
参考図書はこちらです。
また、以下の記事も参考にさせていただきました。
データの準備
本書 P.16に掲載されている身長データ(図表1-1)を使用します。
# 身長データ(単位:cm)
height_cm <- c(
151, 154, 158, 162,
154, 152, 151, 167,
160, 161, 155, 159,
160, 160, 155, 153,
163, 160, 165, 146,
156, 153, 165, 156,
158, 155, 154, 160,
156, 163, 148, 151,
154, 160, 169, 151,
160, 159, 158, 157,
154, 164, 146, 151,
162, 158, 166, 156,
156, 150, 161, 166,
162, 155, 143, 159,
157, 157, 156, 157,
162, 161, 156, 156,
162, 168, 149, 159,
169, 162, 162, 156,
150, 153, 159, 156,
162, 154, 164, 161
)データ数nを確認します。
# データ数の確認
n <- length(height_cm)
n## [1] 80したがって、データ数はn=80 です。
度数分布表の作成
身長データの度数分布表の作成方法については、以下の記事で詳しく説明しています。

度数分布表を作成(Rコード)
#階級の対象範囲
start_val <- 140
end_val <- 170
#階級幅とoffset
class_interval <- 5
offset <- 0.5
#階級境界の設定
class_breaks <- seq(
from = start_val + offset,
to = end_val + offset,
by = class_interval
)
class_breaks
#階級ラベルの作成
lower_bounds <- floor(class_breaks[-length(class_breaks)]) +1 #各階級の下端
upper_bounds <- floor(class_breaks[-1]) #各階級の上端
lower_bounds
upper_bounds
class_labels <- paste(
lower_bounds,
upper_bounds,
sep = "-"
)
class_labels
#階級値の設定
class_marks <- (lower_bounds + upper_bounds) / 2
class_marks
#階級の割り当て
height_class <- cut(
height_cm,
breaks = class_breaks,
labels = class_labels,
include.lowest = TRUE,
right = TRUE
)
height_class
#度数の集計
class_freq <- table(height_class)
class_freq
#データフレームとして整形
freq_df <- data.frame(
class_labels = class_labels,
class_marks = class_marks,
freq = as.integer(class_freq)
)
freq_df
#相対度数
relative_freq <- freq_df$freq / sum(freq_df$freq)
relative_freq
freq_df$relative_freq <- relative_freq
freq_df以下では、この度数分布表をもとに議論を進めます。
## class_labels class_marks freq relative_freq
## 1 141-145 143 1 0.0125
## 2 146-150 148 6 0.0750
## 3 151-155 153 19 0.2375
## 4 156-160 158 30 0.3750
## 5 161-165 163 18 0.2250
## 6 166-170 168 6 0.0750平均値とは
平均値(mean)は、「データの合計を、データ数で割ったもの」として定義されます。
# 平均値(mean)
mean_height_cm <- sum(height_cm) / n
mean_height_cm## [1] 157.575これは、生データから直接計算した「真の平均値」です。
度数分布表から平均値を計算する
次に、度数分布表のみを使って平均値を求めることを考えます。
結論としては、各階級の「階級値×相対度数」を計算し、その合計を求めることで、平均値の近似を得ることができます。
#階級値×相対度数
class_mark_x_relative_freq <- class_marks * relative_freq
class_mark_x_relative_freq
#平均値の近似
approx_mean_height_cm <- sum(class_mark_x_relative_freq)
approx_mean_height_cm## [1] 1.7875 11.1000 36.3375 59.2500 36.6750 12.6000
## [1] 157.75先に計算した平均値「157.575」と比較すると、階級値×相対度数の合計「157.75」は非常に近い値であることがわかります。
なぜ平均値の近似が得られるのか
相対度数は、以下のように定義されます。
$$ 相対度数_i = \frac{度数_i}{全体のデータ数n} $$
したがって、階級値×相対度数の合計の計算は、以下の式変形が可能です。
$$
\begin{eqnarray*}
\sum_{i} (\text{階級値}_i \times \text{相対度数}_i)
&=& \sum_{i} \left(\text{階級値}_i \times \frac{\text{度数}_i}{n}\right) \\
&=& \frac{1}{n} \sum_{i} (\text{階級値}_i \times \text{度数}_i) \\
&\approx& \text{平均値}
\end{eqnarray*}
$$
各階級に属するデータを全てその階級の代表値(階級値)に置き換えたと考えると、それに各階級の度数を掛け合わせることで、「全データの(仮想的な)合計」であると解釈できます。
この「仮想的な合計」を全データ数nで割ることで「生データを階級値で近似した場合の平均値」が得られる、というわけです。
このようにして計算される平均値を「加重平均(weighted mean)」といいます。
度数分布表の読み方
上記を踏まえて、度数分布表の読み方を整理します。
たとえば、第4階級「156–160」には 30 個のデータがあります。
- 156~160 cmの身長の人が30人いる(実際のデータから直接読み取れる事実)
- 158 cmちょうどの身長の人が30人いる(階級値を用いた近似的な解釈)
このように考えることで、度数分布表から平均値を近似的に求めることが可能になります。
ヒストグラムと平均値
身長データのヒストグラムを作成すると、以下のようになります。
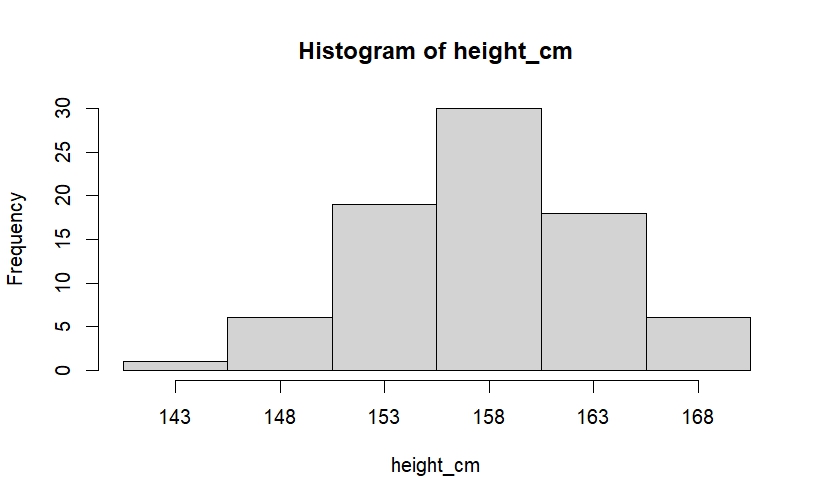
ヒストグラムを作成(Rコード)
#ヒストグラム
hist(
height_cm,
breaks = class_breaks,
include.lowest = TRUE,
right = TRUE,
xaxt = "n"
)
axis(
side = 1,
at = class_marks,
labels = class_marks
)このヒストグラムに、度数分布表から計算した平均値(157.75)の位置を破線で示すと、以下のようになります。
# 平均値の位置に垂直線(破線)を引く
abline(
v = approx_mean_height_cm, # 平均値の位置
col = "red", # 線の色
lwd = 2, # 線の太さ
lty = 2 # 破線
)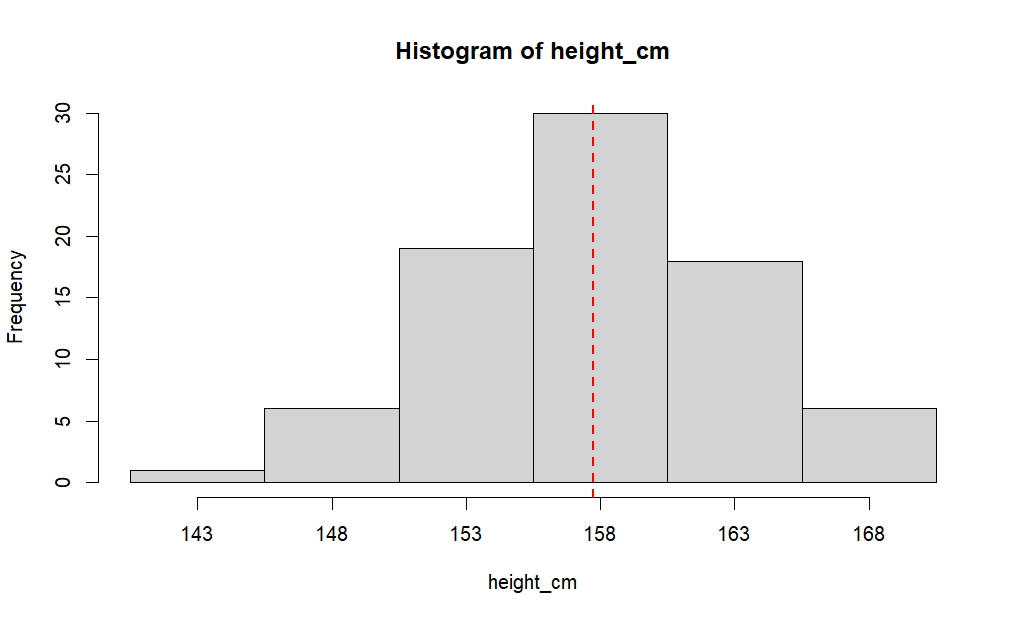
ヒストグラム上で平均値が持つ意味を考えると、「ヒストグラムを”やじろべえ”と見なしたときのつり合いの支点(重心)」であると捉えることができます。
平均値の捉え方
本書では、平均値の特徴を次の3点に整理しています。
- 分布するデータを代表する1点である(データは平均値の周囲に分布している)
- 多く現れるデータほど平均値への影響が大きい
- ヒストグラムが左右対称の場合、平均値は対称軸上に位置する
まず、平均値は「代表値」の一つであり、通常はデータが分布している範囲の中に位置します。この点は、ヒストグラムを「やじろべえ」と見なしたときの重心を思い浮かべると理解しやすいです。
次に、平均値は「階級値 × 相対度数」を全階級について足し合わせて計算されます。そのため、度数が多い階級ほど相対度数が大きくなり、平均値に与える影響も大きくなります。。
最後に、ヒストグラムが左右対称な形をしている場合、左右の重さがつり合うため、平均値(重心)はちょうど中央の位置に現れます。この点も、やじろべえのイメージを使うと直感的に理解できます。
練習問題
本書 P.30に掲載されている架空のデータから、上記と同じ方法で度数分布表を作成し、平均値を計算します。
# 架空データ
class_marks <- c(30, 50, 70, 90, 110, 130) #階級値
freq <- c(5, 10, 15, 40, 20, 10) #度数結果は、以下のようになりました。
#相対度数
relative_freq <- freq / sum(freq)
#階級値×相対度数
class_mark_x_relative_freq <- class_marks * relative_freq
#データフレームに変換して整形
freq_df <- data.frame(
class_marks,
freq,
relative_freq,
class_mark_x_relative_freq
)
freq_df
#平均値の計算
sum(freq_df$class_mark_x_relative_freq)## class_marks freq relative_freq class_mark_x_relative_freq
## 1 30 5 0.05 1.5
## 2 50 10 0.10 5.0
## 3 70 15 0.15 10.5
## 4 90 40 0.40 36.0
## 5 110 20 0.20 22.0
## 6 130 10 0.10 13.0
## [1] 88まとめ
今回の記事では、度数分布表を用いて平均値を近似的に求める方法を、Rによる実装とあわせて整理しました。
生データが手元にない場合や、分布の形と代表値の関係を考えたい場合に、平均値を「階級値 × 相対度数」の合計として求める考え方は有効です。
これは、本書でも強調されている重要なポイントです。
この計算、(階級値×相対度数の合計)は、統計学の全体にわたって使われるものなので、よく記憶に留めておいてほしいと思います。できれば、この計算が自然に思えるまで、しっかりと頭に入れてもらいたいのです。
小島寛之『完全独習 統計学入門』P.26
度数分布表から平均値を求めるという今回の内容は、単なる計算手法にとどまらず、「平均値とは何か」「代表値とはどのような意味を持つのか」を理解するための基礎になります。
今回に限らず、今後統計学を学ぶうえでも、この考え方を意識しながら理解を深めていきたいところです。



